Part I - Basics
Bayes Rule and Total Probability
A random experiment is one whose outcome is uncertain and which can be repeated indefinitely under essentially identical conditions. Examples are rolling a die, tossing a coin, making a laboratory measurement with a degree of uncontrollable error.
The sample space of a random experiment is the set of all its possible outcomes. We will denote the sample space by the Greek letter Ω (upper-case Omega). Individual outcomes of an experiment will be denoted generically by ω (lower-case Omega). For example, in the experiment of tossing a six-sided die and observing the number of spots, the sample space might be described as Ω={1,2,3,4,5,6}.
A population is a set of individuals or objects that forms the subject of a statistical investigation. Usually, the population is so large that it is not feasible to examine every member of the population and a smaller subset (called a sample) is chosen to represent the population. In such cases, the sample space is not the population. Rather, it is the collection of all samples (subsets of the population) of a given size.
An event is a subset of the sample space. Events may be described in mathematical notation or in informal ordinary language. For example, the event E="The number of spots is even." is also E={2,4,6}. Events are denoted generically by upper-case Latin letters, such as "E" above.
If ω is the outcome of a random experiment, the event E occurs if weE.
1. The complement of E, denoted Ec, occurs if and only if E does not occur. In other words,
![]()
2. The union of a finite or infinite sequence of events is an event. The union occurs if and only if at least one of the individual events in the sequence occurs.
![]()
3. The entire sample space Ω is an event (the certain event). The certain event arises naturally when an ordinary language description of an event is satisfied by every outcome of the random experiment.
4. The empty set φ is an event. The empty event arises naturally when an ordinary language description cannot be satisfied by any outcome of the random experiment. Note that
![]()
5. The intersection of a finite or infinite sequence of events in an event. The intersection occurs if and only if each of the individual events in the sequence occurs.
![]()
If E1∩E2 = φ, the events E1 and E2 are said to be disjoint. This means that they cannot both occur.
A probability assignment or probability measure is a way of assigning probabilities between 0 and 1 to events. In other words, it is a function P whose domain is the set of all events associated with a random experiment and whose codomain is the unit interval [0, 1]. A probability assignment is an essential part of modeling a random experiment. Ideally, it comes from a detailed background knowledge of the phenomena of the experiment. Probability theory is the study of the mathematical consequences of the basic properties (axioms) of probability assignments given in the next paragraph. Statistics is the study of methods of using data to assess the correctness of probability models of real life experiments.
Many random experiments have only a finite number of possible outcomes. For such an experiment, let n denote the number of possible outcomes. A singleton event is an event that consists of only one outcome ω. Denote this event by {ω}. The experiment is said to have equally likely outcomes if P({ω}) = 1/n for all ω. It then follows from the basic rules of probability that for any event E,

where #(E) is the number of outcomes in the event E. The assumption of equally likely outcomes may or may not be appropriate for a given experiment. We almost always assume equally likely outcomes for certain simple experiments involving tossing dice, drawing cards, etc.
If a finite population has M members, a sample without replacement of size m is simply a subset of size m of the population. The number of such subsets is

where, e.g., M! (M factorial) is the product of the positive integers from 1 to M, inclusive. Consider a random experiment whose outcome is a subset of size m from the population. If all outcomes are equally likely, the probability of each singleton event {ω} is given by
I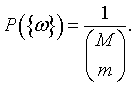
This is what is usually meant by "choosing a random sample of size m". Sometimes the order of presentation of the population members selected is important. In these cases, the outcome of the experiment is a non-repeating sequence (not just a subset) of length m from the population. These are also called permutations of length m from the population. The number of permutations of length m is
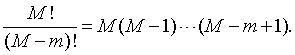
If all permutations of length m are equally likely, the result of the experiment is called an ordered sample without replacement from the population.
An ordered sample of size m, with replacement, from a population is a possibly repeating sequence of length m from the population. The number of such sequences is Mm. It is not hard to see that if the sample size m is much less than the population size M, a very large fraction of the ordered samples with replacement will not repeat themselves anyway, so there is little practical difference between ordered sampling with and without replacement. In such circumstances, samples without replacement are often treated as samples with replacement for mathematical convenience.
Probabilities discussed up to this point have been unconditional probabilities. If D and E are events and P(E) > 0, the conditional probability of D, given that E occurs, is
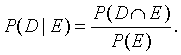
If the experiment has equally likely outcomes, P(D|E) is just the fraction of all the outcomes in E where D also occurs. Two events D and E are independent if P(D∩E) = P(D)P(E). If P(E) > 0, this is equivalent to P(D|E) = P(D), i.e., the conditional probability of D given E is the same as the unconditional probability of D. For example, in the experiment of drawing a single card from a standard deck with equally likely outcomes, the events "Draw a Heart" and "Draw a Queen" are independent. The events "Draw a Heart" and "Draw a red card" are not independent. They are dependent.
Let E1, E2, ..., Ek be pairwise disjoint events such that P(Ei) > 0 for each i and
![]()
This means that one of the events Ei must occur and that only one can occur. Let D be another event. The law of total probability says that
![]()
and Bayes' rule says that
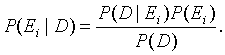
For example, let D denote a set of symptoms exhibited by a patient and let E1, E2, ..., Ek be a collection of mutually exclusive disease conditions that might account for the symptoms. For each disease Ei, there is a certain probability P(D|Ei) that a sufferer of that disease will have the symptoms D and there is a certain probability P(Ei) that a patient will have that specific disease. Then Bayes' rule gives the probability that the patient has the specific disease, given that he or she has the symptoms D.