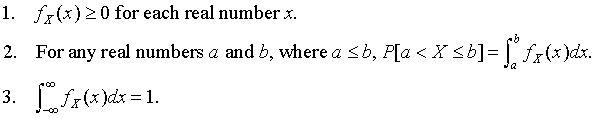
Part IV- Continuous Distributions
Relationship Between Density and Distribution Functions
Expected Values, Means and Variances
A Table of Continuous Distributions
Aside from the discrete distributions, the most important class of distributions are those of continuous type. A random variable X with a continuous distribution has an associated density function, which is a function fX with the following properties:
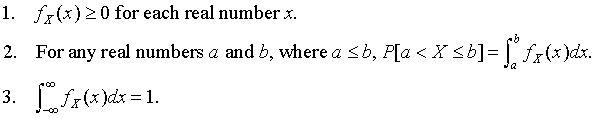
The word "continuous" is being slightly abused here. These conditions are stronger than mere continuity of the cumulative distribution function. There are distributions that are neither discrete nor of this type, but they are of minor importance and will not be discussed. In condition (2) above, either or both of the end points a and b can be included in or excluded from the interval without changing the probability. This is because for a continuous random variable, P[X = a]=P[X = b]=0.
The cumulative distribution function is the integral of the density function. Specifically,
![]()
for each real number x. The fundamental theorem of calculus then implies that
![]()
is a density function if FX has a continuous derivative.
If X has a density function fX and g(x) is a real valued function, the expected value of g(X) is defined as
![]()
provided that the integral exists. If we let g(x) ≡ x, we get the mean of the random variable, again denoted by the Greek letter μ.
![]()
If we let g(x) ≡ (x-μ)2, we get the variance of X, denoted by σ2.
![]()
The standard deviation σ is the square root of the variance.
A random variable X has the uniform distribution on the interval (a, b) if its density function is given by
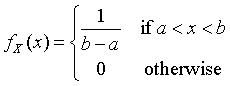
The values of the density function at the endpoints a and b are immaterial. The special case where a = 0 and b = 1 is called the standard uniform distribution on (0, 1).
All other uniform distributions are related to the standard uniform distribution on (0, 1) as follows. If U is a random variable uniformly distributed on (0, 1) and if a < b, then X=a + (b-a)U is uniformly distributed on (a, b). Conversely, if X is uniformly distributed on (a, b), then U = (X-a)/(b-a) is uniformly distributed on (0, 1).
The mean of the uniform distribution on (a, b) is
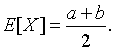
Its variance is
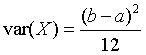
The graph of the standard uniform density function is shown below.

Every distribution is related to the standard uniform distribution. If F is a given cumulative distribution function, U is a random variable uniformly distributed on (0, 1), and the equation U = F(X) can be solved uniquely for X, then the random variable X has the cumulative distribution function F.
A random variable X has an exponential distribution if it has a density function of the form
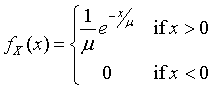
The parameter μ is a positive number. In fact, it is both the mean and the standard deviation of this distribution.
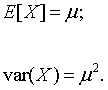
The exponential distribution with mean μ = 1 is the standard exponential distribution. It is related to all other exponential distributions in the following way. If Y has the standard exponential distribution and μ is any positive number, then X = μY has the exponential distribution with mean μ. Conversely, if X has the exponential distribution with mean μ, then Y = X/μ has the standard exponential distribution.
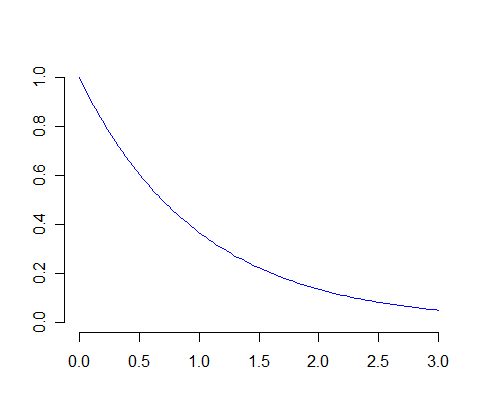
The graph of the standard exponential density function is pictured below.
The gamma function is one of the special functions of mathematics. For a positive argument α its value is defined as
![]()
Using integration by parts, it is not difficult to show that the gamma function satisfies the identity
![]()
Furthermore, G(1) =1 and therefore, for a positive integer n, G(n) = (n-1)!. A random variable X has the gamma distribution with shape parameter α > 0 and scale parameter β > 0 if its density function is
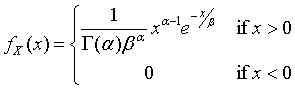
The mean and variance of the gamma distribution are given in terms of the shape and scale parameters by
, 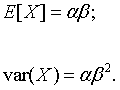
The exponential distributions are a special class of gamma distributions with α = 1 and β = μ.
The graph of the gamma density function with α = 3 and β = 1 is shown below.

If the random variable X has the standard exponential distribution and we define a new random variable Y by
![]()
where α and β are positive constants (parameters), then the distribution of Y is called a Weibull distribution. Its density function is given by
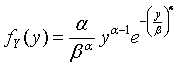
Its mean and variance are given by
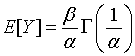
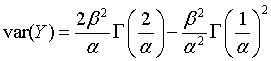
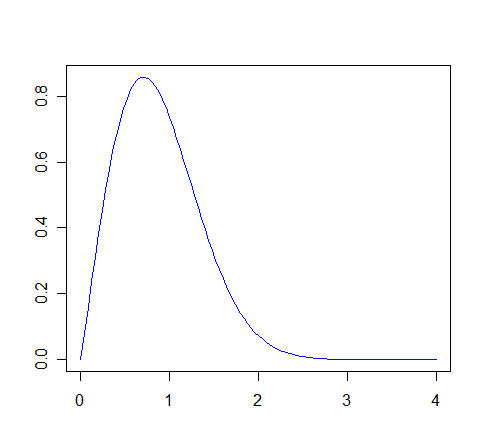
The Weibull distributions are especially useful in modeling lifetimes of components in engineering systems. The graph of the Weibull density with α = 2 and β = 1 is shown below.
A gamma distribution with shape parameter α = m/2, where m is a positive integer, and scale parameter β = 2 is called a chi-square distribution with m degrees of freedom (d.f.). The mean of this distribution is m and the variance is 2m. Chi-square distributions are very important in statistical inference.
Normal distributions are the most important distributions in classical probability and statistics. A random variable X has the normal distribution with mean μ and standard deviation σ if its density function is
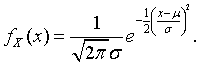
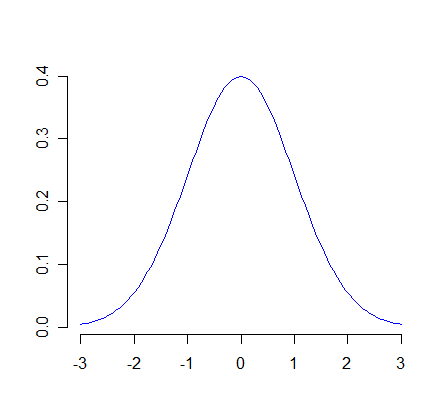
As the terminology indicates, the mean of the distribution is the parameter μ and the variance is σ2. The particular case where μ = 0 and σ = 1 is especially important. It is the standard normal distribution. A random variable Z has the standard normal distribution if its density function is
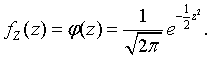
All normal distributions are related to the standard normal distribution in the following way: If Z has a standard normal distribution and if μ and σ > 0 are any numbers, then X= σZ + μ has the normal distribution with mean μ and standard deviation σ. Conversely, if a random variable X has the normal distribution with mean μ and standard deviation σ, then Z = (X-μ)/σ has the standard normal distribution. This is extremely important because it implies that tabulated values of the standard normal distribution can be used for any normal distribution.
The standard normal distribution is also of great importance because of the central limit theorem. The standard normal density function is pictured below.
|
Name |
Density Function |
Mean |
Variance |
Relationships |
|
Uniform |
|
|
|
All others |
|
Exponential |
|
μ |
μ2 |
|
|
Gamma |
|
|
|
|
|
Weibull |
|
|
|
|
|
Chi-Square |
Gamma with α = m/2, β = 2 m a positive integer (degrees of freedom) |
m |
2m |
|
|
Normal |
|
μ |
σ2 |
All others (central limit theorem) |
|
Standard Normal |
|
0 |
1 |