HJM, Vol. 47, No. 1, 2021

HOUSTON JOURNAL OF
MATHEMATICS

 Electronic Edition Vol. 47, No. 1, 2021

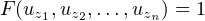
Editors:  D. Bao (San Francisco, SFSU), D. Blecher (Houston), B. G. Bodmann (Houston), H. Brezis (Paris and Rutgers), B.  Dacorogna (Lausanne), M. Dugas (Baylor), M. Gehrke (LIAFA, Paris7), C. Hagopian (Sacramento), R. M. Hardt (Rice), S. Harvey (Rice), A. Haynes (Houston), Y. Hattori (Matsue, Shimane), W. B. Johnson (College Station),  M. Rojas (College Station), Min Ru (Houston), S.W. Semmes (Rice), D. Werner (FU Berlin).
Managing Editors: B. G. Bodmann and K. Kaiser (Houston)

 Houston Journal of Mathematics


Contents

J.R. Juett, Department of Computer Studies and Mathematics, University of Dubuque, 2000 University Avenue, Dubuque, IA 52001 (jjuett@dbq.edu), and Christopher Park Mooney, Department of Mathematics, Statistics, and Computer Science, University of Wisconsin - Stout, 712 South Broadway Street, Menomonie, WI 54751 (mooneych@uwstout.edu).
Notions of unique factorization in commutative rings with zero divisors, pp. 1–29.

ABSTRACT. In recent decades, mathematicians have extended the definition of a unique factorization domain to rings with zero divisors in many different ways, by mixing and matching different notions of “irreducible” elements, “equivalent” factorizations, and “redundant factorizations” from the literature and deciding which elements are required to have “unique factorizations.” Their study raises many natural questions such as how many distinct kinds of “unique factorization rings” one can obtain through this approach, which combinations of choices lead to equivalent notions, and if one can find nice structural characterizations of each of these notions. This paper will be answering these questions.  

James Evans, School of Mathematical and Physical Sciences, University of Newcastle, University Drive, Callaghan NSW 2308, Australia (james.evans10@uon.edu.au).
The Ghost Measures of Affine Regular Sequences, pp. 31–50.

ABSTRACT. The family of k-regular sequences exhibits self-similar behaviour between powers of k. One way to study this self-similarity is to attempt to describe the limiting shape of the sequence using measures, which results in an object which we call the ghost measure. The aim of this paper is to explicitly calculate this measure and some of its properties, including its spectral type, for the general family of affine 2-regular sequences.  

Er-Guang Yang, School of Mathematics & Physics, Anhui University of Technology, Maanshan 243002, P.R. China (egyang@126.com).
Set-valued maps and some generalized metric spaces, pp. 51–61.

ABSTRACT. To characterize countably paracompact spaces with set-valued maps, Yamazaki introduced the notion of strictly increasing closed cover of a topological space. In this paper, we show that most of generalized metric spaces can be characterized with set-valued maps with values into the family of all closed nonempty subsets of a space which has a strictly increasing closed cover.  

B. V. Rajarama Bhat, Theoretical Statistics and Mathematics Unit, Indian Statistical Institute, R. V. College Post, Bangalore-560059, India (bhat@isibang.ac.in), and Mithun Mukherjee, School of Mathematical & Computational Sciences, Indian Association for the Cultivation of Science, Jadavpur, Kolkata, 700032, India (mithun.mukherjee@iacs.res.in).
Two states, pp. 63–95.

ABSTRACT. D. Bures defined a metric β on states of a C∗-algebra and this concept has been generalized to unital completely positive maps ϕ : A→ℬ, where ℬ is either an injective C∗-algebra or a von Neumann algebra. We introduce a new distance γ for the same classes of unital completely positive maps. We use in our definition the distance between representations on the same Hilbert C∗-module in contrast to the Bures metric which uses one representation and distinct vectors. This metric can be expressed in terms of a class of completely positive maps on free products of C∗-algebras and in this setting γ looks like Wasserstein metric on probability measures. Surprisingly, when the range algebra ℬ is injective, γ and β are related by the following explicit formula: β2 = 2 −∘ ----2- 4− γ. 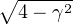A deep result of Choi and Li on constrained dilation is the main tool in proving this formula.  

Yu Zhou, School of Mathematics, Physics and Statistics, Shanghai University of Engineering Science, Shanghai, 201620, China (roczhou−fly@126.com).
Representation of surjective additive isometric embeddings between Hausdorff metric spaces of certain bounded closed convex subsets of Banach spaces, pp. 97–114.

ABSTRACT. Let X and Y be real infinite-dimensional Banach spaces, B(X) be the closed unit ball X, cc(X) be the set of all nonempty compact convex subsets of X, ℰX ≡{co[∪i=1n(Ai + riB(X))] : Ai ∈ cc(X),ri ≥ 0,1 ≤ i ≤ n,n ∈ ℕ} and f be a surjective isometric embedding from the Hausdorff metric space (ℰX,H) onto the Hausdorff metric space (ℰY ,H) satisfying that f(E + F) = f(E) + f(F) for any pair E,F ∈ℰX. Then, there is a surjective linear isometric embedding f : X → Y such that f(E) = {f(e) : e ∈ E} for every E ∈ℰX.  

Saeid Zahmatkesh, Department of Mathematics, Faculty of Science, King Mongkut’s University of Technology Thonburi, Bangkok 10140, THAILAND (saeid.zk09@gmail.com, saeid.kom@kmutt.ac.th).
The Nica-Toeplitz algebras of dynamical systems over abelian lattice-ordered groups as full corners, pp. 115–149.

ABSTRACT. Consider the pair (G,P) consisting of an abelian lattice-ordered discrete group G and its positive cone P. Let α be an action of P by extendible endomorphisms of a C∗-algebra A. We show that the Nica-Toeplitz algebra Tcov(A ×αP) is a full corner of a group crossed product ℬ ⋊ βG, where ℬ is a subalgebra of ℓ∞(G,A) generated by a collection of faithful copies of A, and the action β on ℬ is given by the shift on ℓ∞(G,A). By using this realization, we show that the ideal ℐ of Tcov(A ×αP) for which the quotient algebra Tcov(A ×αP)∕ℐ is the isometric crossed product A ×αisoP is also a full corner in an ideal J ⋊ βG of ℬ ⋊ βG.  

Marco Antonio Lázaro Velásquez, Departamento de Matemática, Universidade Federal de Campina Grande, 58.409-970 Campina Grande, Paraíba, Brazil (marco.velasquez@mat.ufcg.edu.br).
A half-space property for strongly 1-stable hypersurfaces with constant second mean curvature in the Euclidean sphere, pp. 151–164.

ABSTRACT. We investigate the strong 1-stability of closed hypersurfaces with constant second mean curvature in the Euclidean sphere. Initially, under a suitable restriction on the mean curvature, we prove that if such a hypersurface is strongly 1-stable, then it must be a certain geodesic sphere. Afterwards, we obtain a nonexistence result concerning these hypersurfaces.  

Gabriele Bonanno, Department of Engineering, University of Messina, c.da Di Dio Sant’Agata 98166 - Messina (Italy) (bonanno@@unime.it), and Roberto Livrea, Department of Mathematics and Computer Sciences, University of Palermo, via Archirafi 34, 90123 - Palermo (Italy) (roberto.livrea@unipa.it).
A proof of the Ghoussoub-Preiss theorem by the ε−perturbation of Brezis-Nirenberg, pp. 165-191.

ABSTRACT. In this note, a proof of the Ghoussoub-Preiss theorem is presented by using the ε−perturbation as introduced by Brezis-Nirenberg. Thus, besides the deformation lemma, other advanced tools such as the Radon measures space, sub-differential, or the theory of non-differentiable functions, are avoided. Our new argument is a lemma of local type which is used in combination with other main ingredients like the Ekeland variational principle and the pseudo-gradient lemma, for which a new proof is proposed as a consequence of the Michael selection theorem.  

Qiong Wang, School of Sciences, Chongqing University of Posts and Telecommunications, Chongqing, 400065, P.R. China (qiongwangsdu@126.com), Wei Chen, School of Sciences, Chongqing University of Posts and Telecommunications, Chongqing, 400065, P.R. China (weichensdu@126.com), and Guoping Zhan, Department of Mathematics, Zhejiang University of Technology, Hangzhou, 310023, Zhejiang, P. R. China (zhangp@zjut.edu.cn).
Factorization of linearly independent operators and prime solutions of partial differential equations, pp. 193-209.

ABSTRACT. In this paper, we obtain the precise form of meromorphic functions u(z1,z2) in ℂ2 when the linearly independent operators auz1 + buz2 and cuz1 + duz2 have a common right factor with constants a,b,c,d. We also describe entire solutions of the partial differential equation
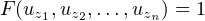
F (uz ,uz ,...,uz ) = 1 1 2 n
in ℂn under a more general definition in the sense of the prime functions. In addition, our results generalize the recent results in a work by Li.  

Xin Liu, Institute of Mathematics, Ningde Normal University, Ningde, Fujian 352100, P.R. China (liuxintp@126.com), and Chuan Liu, Department of Mathematics, Ohio University Zanesville Campus, Zanesville, OH 43701, USA (liuc1@ohio.edu).
Notes on spaces with certain point-countable families , pp. 211-222.

ABSTRACT. In this paper, we discuss some properties of spaces with certain point-countable families and the following examples are provided, which answer several questions posed by T. Banakh and L. Zdomskyy, and S. Lin and Z.Y. Cai, respectively:

(1) There exists a quotient s-image of a metric space which does not have countable pseudocharacter.

(2) There exists a closed and non-boundary-s-mapping f : X → Y such that X has a compact-countable base and Y contains no closed copy of Sω1.

(3) There is a sequence-covering mapping f from a space X with a countable sn-network onto a space Y such that f is not a 1-sequence-covering mapping.
And following result is proved:

Let {Xn}n∈ℕ be a family of k-spaces with point-countable k-networks. Then every subspace with countable fan-tightness in the product space ∏ n∈ℕXn has a point-countable base.

Finally, we give a negative answer to Cai and Lin’s question under property CH.

Nikita Agarwal, Department of Mathematics, Indian Institute of Science Education and Research Bhopal, Bhopal Bypass Road, Bhauri, Bhopal 462 066, Madhya Pradesh, India (nagarwal@iiserb.ac.in), Soumya Dey, The Institute of Mathematical Sciences, IV Cross Road, CIT Campus, Taramani, Chennai 600 113, Tamil Nadu, India (soumya.sxccal@gmail.com), Neeraj K. Dhanwani, Department of Mathematics, Indian Institute of Science Education and Research Bhopal, Bhopal Bypass Road, Bhauri, Bhopal 462 066, Madhya Pradesh, India (nkd9335@iiserb.ac.in), and Kashyap Rajeevsarathy, Department of Mathematics, Indian Institute of Science Education and Research Bhopal, Bhopal Bypass Road, Bhauri, Bhopal 462 066, Madhya Pradesh, India (kashyap@iiserb.ac.in).
Liftable mapping class groups of regular cyclic covers, pp. 223-243.

ABSTRACT. Let Mod(Sg) be the mapping class group of the closed orientable surface of genus g ≥ 1. For k ≥ 2, we consider the standard k-sheeted regular cover pk : Sk(g−1)+1 → Sg, and analyze the liftable mapping class group LModpk(Sg) associated with the cover pk. In particular, we show that LModpk(Sg) is the stabilizer subgroup of Mod(Sg) with respect to a collection of vectors in H1(Sg, ℤk), and also derive a symplectic criterion for the liftability of a given mapping class under pk. As an application of this criterion, we obtain a normal series of LModpk(Sg), which generalizes a well known normal series of congruence subgroups in SL(2, ℤ). Among other applications, we describe a procedure for obtaining a finite generating set for LModpk(Sg) and examine the liftability of certain finite-order and pseudo-Anosov mapping classes.  

Isaac Adjei, Department of Mathematical Sciences, University of South Africa, P. O. Box 392, 0003 Pretoria, SOUTH AFRICA (isadjei@yahoo.com), and Themba Dube, Department of Mathematical Sciences, University of South Africa, P. O. Box 392, 0003 Pretoria, SOUTH AFRICA (dubeta@unisa.ac.za).
The Banaschewski extension and some variants of openness, pp. 245-261.

ABSTRACT. If X is a zero-dimensional Hausdorff space, let ζX be its Banaschewski compactification. Every continuous map f : X → Y between zero-dimensional Hausdorff spaces has a Banaschewski extension, fζ: ζX → ζY , which is a unique continuous map making the square
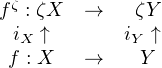
fζ : ζX → ζY iX ↑ iY ↑ f : X → Y

commute, where the vertical maps are inclusions. We give a characterisation of when fζ is nearly open in the sense of V. Pták. The technique used also yields (via simple adaptation) a necessary and sufficient condition for the Stone extension, fβ: βX → βY , of any continuous map f : X → Y between Tychonoff spaces to be nearly open.

Marcela López, Departamento de Matemáticas, Universidad Autónoma Metropolitana, Av. San Rafael Atlixco 186, Col. Vicentina, Del. Iztapalapa, C.P. 09340, Mexico City, Mexico (kier_93@hotmail.com), and Iván Sánchez, Departamento de Matemáticas, Universidad Autónoma Metropolitana, Av. San Rafael Atlixco 186, Col. Vicentina, Del. Iztapalapa, C.P. 09340, Mexico City, Mexico (isr.uami@gmail.com).
Lindelöfness and Čech-completeness in the construction of Hartman-Mycielski, pp. 263-270.

ABSTRACT. Let G be a topological group and G∙ the group of Hartman-Mycielski associated to G. We mainly prove that G∙ is Lindelöf if and only if Gn is Lindelöf for every natural number n. We also show that G∙ is Čech-complete if and only if |G| = 1. These results answer some items of A.V. Arhangel’skii and M.G. Tkachenko.