HOUSTON JOURNAL OF
MATHEMATICS
Electronic Edition Vol. 47, No. 3, 2021
Editors: D. Bao (San Francisco, SFSU), D. Blecher
(Houston), B. G. Bodmann (Houston), H. Brezis (Paris and Rutgers),
B. Dacorogna (Lausanne), M. Dugas (Baylor), M.
Gehrke (LIAFA, Paris7), C. Hagopian (Sacramento), R. M. Hardt (Rice), S. Harvey (Rice), A. Haynes (Houston), Y. Hattori
(Matsue, Shimane), W. B. Johnson (College Station), M. Rojas (College Station),
Min Ru (Houston), S.W. Semmes (Rice), D. Werner (FU Berlin).
Managing Editors: B. G. Bodmann and K. Kaiser (Houston)
Houston Journal of Mathematics
Contents
Martin Avendano, Centro Universitario de la Defensa, Academia General Militar,
Ctra. de Huesca s/n., 50090, Zaragoza, Spain (avendano@unizar.es), and Jorge
Martín-Morales, Centro Universitario de la Defensa, Academia General Militar,
Ctra. de Huesca s/n., 50090, Zaragoza, Spain (jorge@unizar.es).
Bivariate trinomials over finite fields, pp. 535–552.
ABSTRACT. We study the number of points in the family of plane curves
defined by a trinomial with fixed exponents and varying coefficients over finite
fields. We prove that each of these curves has an almost predictable number of
points, given by a closed formula that depends on the coefficients, the exponents,
and the field, with a small error term for which we provide an upper bound in
terms of an analog of the genus and the size of the field. We obtain these upper
bounds from some linear and quadratic identities that the error terms satisfy.
These identities are, in some cases, strong enough to determine the error terms
completely.
Yupei Wu, School of Mathematical Sciences, Nanjing Normal University, Nanjing
210023, P. R. China (1355716673@qq.com), and Yan Xu, School of Mathematical
Sciences, Nanjing Normal University, Nanjing 210023, P. R. China (xuyan@njnu.edu.cn).
A further result on normal families and exceptional functions, pp. 553–569.
ABSTRACT. Let k ≥ 3 be a positive integer, A > 1 be a constant, and φ(z)(⁄≡ 0) be a
function holomorphic in a domain D, and let ℱ be a family of meromorphic functions
defined in D. If, for every function f ∈ℱ, f has only zeros of multiplicity at least k and
satisfies: (a) f(z) = 0 ⇒|f(k)(z)|≤ A|φ(z)|, (b) f(k)(z)≠φ(z), (c) all poles
of f have multiplicity at least 2 for k ≥ 4(3 for k = 3), then ℱ is normal in
D.
Xiaoqing Lu, Mathematics and Information Technology School, Jiangsu Second Normal
University, Beijing West Road 77, Nanjing, 210013, P. R. China (luxiaoqing1984@126.com),
and Liangwen Liao, Department of Mathematics, Nanjing University, Hankou Road 22,
Nanjing, 210093, P. R. China (maliao@nju.edu.cn).
Meromorphic solutions of a certain type of nonlinear differential equations, pp.
571–584.
ABSTRACT. We consider transcendental meromorphic solutions with N(r,f) = S(r,f)
of the following type of nonlinear differential equations:
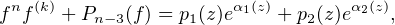 where n ≥ 3, k ≥ 2 are positive integers, Pn−3(f) is a differential polynomial in f of
degree not greater than n− 3, α1(z), α2(z) are nonconstant entire functions, p1(z), p2(z)
are nonzero small functions of both eα1(z) and eα2(z).
where n ≥ 3, k ≥ 2 are positive integers, Pn−3(f) is a differential polynomial in f of
degree not greater than n− 3, α1(z), α2(z) are nonconstant entire functions, p1(z), p2(z)
are nonzero small functions of both eα1(z) and eα2(z).
Libing Huang, School of Mathematical Sciences and LPMC, Nankai University, Tianjin
300071, P. R. China (huanglb@nankai.edu.cn), and Zhongmin Shen, Department of
Mathematical Sciences, Indiana University-Purdue University, Indianapolis, IN
46202-3216, USA (zshen@math.iupui.edu).
A conclusive theorem on Finsler metrics of sectional flag curvature, pp. 585–598.
ABSTRACT. If the flag curvature of a Finsler manifold reduces to sectional
curvature, then the manifold can be decomposed into two parts, one part is of
isotropic flag curvature and the other part is an open subset on which the metric is
Riemannian. Moreover, if the sectional flag curvature is negative, then the manifold is
Riemannian.
H. Aruna Kumara, Department of Mathematics, BMS Institute of Technology and Management, Bangalore 560064,
Karnataka, India (arunmathsku@gmail.com), V. Venkatesha, Department
of Mathematics, Kuvempu University, Shankaraghatta, Karnataka 577 451,
India (vensmath@gmail.com), and Devaraja Mallesha Naik, Department of
Mathematics, CHRIST (Deemed to Be University), Bangalore-560029, India
(devaraja.mallesha@christuniversity.in; devarajamaths@gmail.com).
Some results of real hypersurfaces in a complex space form, pp. 599–612.
ABSTRACT. First, we characterize a Hopf real hypersurface admitting gradient almost
Riemann soliton in a non-flat complex space form. Next, we classify real hypersurface of
a non-flat complex space form with W∗⋅ T = 0.
Ruihan Zhang, School of Mathematics and Statistics, Shaanxi Normal University,
Xian, 710119, People’s Republic of China (ruihan@snnu.edu.cn), and Guoxing Ji,
School of Mathematics and Statistics, Shaanxi Normal University, Xian, 710119, People’s
Republic of China (gxji@snnu.edu.cn).
Noncommutative Hp spaces associated with type 1 subdiagonal algebras, pp.
613–622.
ABSTRACT. Let A be a type 1 subdiagonal algebra in a σ-finite von Neumann algebra
ℳ with respect to a faithful normal conditional expectation Φ. We consider a Riesz type
factorization theorem in noncommutative Hp spaces associated with A. It is shown that
if 1 ≤ r,p,q < ∞ such that  =
= 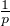 +
+  , then for any h ∈ Hr, there exist h
p ∈ Hp and
hq ∈ Hq such that h = hphq. Beurling type invariant subspace theorem for
noncommutative Lp(1 < p < ∞) space is obtained.
, then for any h ∈ Hr, there exist h
p ∈ Hp and
hq ∈ Hq such that h = hphq. Beurling type invariant subspace theorem for
noncommutative Lp(1 < p < ∞) space is obtained.
Elmiloud Chil, University of Tunis, Institut préparatoire aux études d’ingenieurs de
Tunis 2 Rue Jawaher Lel Nehrou Monflery 1008, TUNISIA (elmiloud.chil@ipeit.rnu.tn),
and Fateh Mekdour, L.A.T.A.O. Faculty of sciences of Tunis, University EL Manar:
Universitary Campus, El Manar TUNISIA (fateh.mekdour@fst.utm.tn).
On lattice homomorphisms in Riesz spaces, pp. 623–632.
ABSTRACT. In this paper, we study the connection between lattice and Riesz
homomorphisms in Riesz spaces. We prove, under a certain condition, that any lattice
homomorphism on a Riesz space is a Riesz homomorphism. This fits with the
type of results by Mena and Roth, Thanh, Lochan and Strauss and Ercan and
Wickstead.
Soumyadip Acharyya, Division of Science, Mathematics, and Engineering,
University of South Carolina Sumter, 200 Miller Road, Sumter, SC 29150, USA
(acharyya@mailbox.sc.edu), Sudip Kumar Acharyya, Department of Pure
Mathematics, University of Calcutta, 35, Ballygunge Circular Road, Kolkata - 700019,
INDIA (sdpacharyya@gmail.com), Rakesh Bharati, Department of Pure Mathematics,
University of Calcutta, 35, Ballygunge Circular Road, Kolkata - 700019, INDIA
(rbharati.rs@gmail.com), and A. Deb Ray, Department of Pure Mathematics,
University of Calcutta, 35, Ballygunge Circular Road, Kolkata - 700019, INDIA
(debrayatasi@gmail.com).
Some algebraic and topological properties of rings of measurable functions, pp.
633–657.
ABSTRACT. For the ring ℳ(X,A) of all real valued measurable functions
over a measurable space (X,A), ℳc(X,A) stands for the subring of ℳ(X,A)
consisting of those functions that have countable range in ℝ. The structure space of
ℳc(X,A) is shown to be homeomorphic to that of ℳ(X,A) and we observe
that within the class of separated realcompact measurable spaces, ℳ(X,A) is
isomorphic to ℳ(Y,ℬ) when and only when ℳc(X,A) is isomorphic to ℳc(Y,ℬ).
We also introduce, via a measure μ on (X,A), three different topologies on
ℳ(X,A), namely the Uμ-topology, UμF-topology and mμF-topology. We establish
a necessary and sufficient criterion for mνF-topology to be weaker than the
mμF-topology. We also give a necessary and sufficient condition for the ring
ℳ(X,A) to be a topological ring (equivalently, a topological vector space) in the
UμF-topology. We further observe that this condition holds if and only if the
mμF-topology on ℳ(X,A) is connected if and only if the pseudonorm topology on
LF(X,A,μ), the set of all weakly essentially bounded functions in ℳ(X,A),
coincides with its relative mμF-topology inherited from ℳ(X,A). Additionally, we
show that a maximal ideal M in ℳ(X,A) is closed in the U-topology if and
only if it is real. Two special subrings of ℳ(X,A), namely ℳF(X,A,μ) and
ℳ∞(X,A,μ), and the associated ideal structures of the parent ring ℳ(X,A) are also
studied.
Chongxia Lu, School of Mathematics and Statistics, Ningbo University, Ningbo,
Zhejiang, 315211, P.R. China (lcx19882012@163.com), and Qingguo Li, College of
Mathematics and Econometrics, Hunan University, Changsha, Hunan, 410082, P.R.
China (liqingguoli@aliyun.com).
Lawson compactness on function spaces of pointed quasicontinuous domains with
property M, pp. 659–670.
ABSTRACT. In this paper, we mainly consider the question of when the Isbell and
Scott topologies coincide on function spaces and investigate the Lawson compactness on
function spaces. The following results are obtained: for a pointed quasicontinuous domain
L with property M and SL-domain X, if X is coherent and algebraic, then the Isbell and
Scott topologies coincide on [X → L]; if X has property M, then the function space
[X → L] is Lawson compact.
Félix Capulín, Universidad Autónoma del Estado de México, Facultad de Ciencias,
Instituto Literario 100, Col. Centro, C.P. 50000, Toluca, Estado de México, México
(fcapulin@gmail.com), David Maya, Universidad Autónoma del Estado de México,
Facultad de Ciencias, Instituto Literario 100, Col. Centro, C.P. 50000, Toluca,
Estado de México, México (dmayae@uaemex.mx, dmayae@outlook.com), Nataly
Mondragón-Chigora, Universidad Autónoma del Estado de México, Facultad de
Ciencias, Instituto Literario 100, Col. Centro, C.P. 50000, Toluca, Estado de México,
México (natich2019@outlook.es), and Fernando Orozco-Zitli, Universidad Autónoma
del Estado de México, Facultad de Ciencias, Instituto Literario 100, Col. Centro, C.P.
50000, Toluca, Estado de México, México (forozcozitli@gmail.com).
Some preserved and reversible properties to the hyperspace of convergent sequences, pp.
671–695.
ABSTRACT. The hyperspace of the nontrivial convergent sequences of a topological
space Hausdorff X is denoted by Sc(X). This hyperspace is endowed with the Vietoris
topology. We consider several generalized metric properties and study the relation
between a space X satisfying such property and its hyperspace Sc(X) satisfying the
same property.
Alejandro Ramírez-Páramo, Facultad de Ciencias de la Electrónica, Benemérita
Universidad Autónoma de Puebla, Río Verde y Av. San Claudio s.n., Puebla,
Pue., México (alejandro.ramirez@correo.buap.mx), and Jesús F. Tenorio, [J.
F. Tenorio]Instituto de Física y Matemáticas, Universidad Tecnológica de la
Mixteca, Carretera a Acatlima, Km 2.5, Huajuapan de León, Oaxaca, México
(jtenorio@mixteco.utm.mx).
A couple of generic theorems in the theory of cardinal functions, pp. 697–709.
ABSTRACT. In this paper we introduce a couple of general technical results which are
tailored to prove some cardinal functions inequalities related to the Arhangel’skiĭ’s
inequality, many of these obtained in recent years. Furthermore, we define the non-γ
number of a space X, denoted by nγ(X), to establish, using one of our generic
theorems, that if X is a T1-space such that nγ(X) ≤ 2(γ,θ)-wLθ(X)χ(X), then
|X|≤ 2(γ,θ)-wLθ(X)χ(X). This result gives a partial positive answer to the question: Is
|X|≤ 2(γ,θ)-wLθ(X)χ(X) if X is Urysohn?
Wei-Feng Xuan, School of Statistics and Mathematics, Nanjing Audit University,
Nanjing, China, 211815 (wfxuan@nau.edu.cn), and Yan-Kui Song, Institute of
Mathematics, School of Mathematical Science, Nanjing Normal University, Nanjing,
China, 210046 (songyankui@njnu.edu.cn).
Quasi-Lindelöf spaces revisited, pp. 711–721.
ABSTRACT. The class of quasi-Lindelöf spaces was introduced by Arhangel’skii and
later studied by Staynova and Song. We say that a topological space X is quasi-Lindelöf
if for any closed subset D ⊂ X and any family U of open sets of X which covers D there
exists a countable subfamily U′⊂U such that D ⊂⋃
U′. In this paper, we prove
that every perfect quasi-Lindelöf space is CCC. Using this result, we obtain a
weakly Lindelöf Moore space which is not quasi-Lindelöf. A Tychonoff example
of weakly Lindelöf non-quasi-Lindelöf space is also given, which has stronger
properties than one given by Song in prior work. We also prove that every
quasi-Lindelöf subspace of the product of finite scattered monotonically normal
spaces has countable extent. Finally, we establish several cardinal inequalities for
quasi-Lindelöf spaces with symmetry g-functions. Some new questions are also
posed.
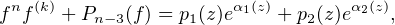
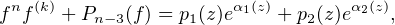
 =
= 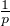 +
+  , then for any h ∈ Hr, there exist h
p ∈ Hp and
hq ∈ Hq such that h = hphq. Beurling type invariant subspace theorem for
noncommutative Lp(1 < p < ∞) space is obtained.
, then for any h ∈ Hr, there exist h
p ∈ Hp and
hq ∈ Hq such that h = hphq. Beurling type invariant subspace theorem for
noncommutative Lp(1 < p < ∞) space is obtained.