HOUSTON JOURNAL OF
MATHEMATICS
Electronic Edition Vol. 48, No. 4, 2022
Editors: D. Bao (San Francisco, SFSU), S. Berhanu (Temple), D. Blecher
(Houston), B. G. Bodmann (Houston), H. Brezis (Paris and Rutgers),
B. Dacorogna (Lausanne), M.
Gehrke (LIAFA, Paris7), R. M. Hardt (Rice), S. Harvey (Rice), A. Haynes (Houston), Y. Hattori
(Matsue, Shimane), W. B. Johnson (College Station), M. Marsh (Sacramento), M. Rojas (College Station),
Min Ru (Houston), S.W. Semmes (Rice), D. Werner (FU Berlin).
Managing Editors: B. G. Bodmann and A. Haynes (Houston)
Houston Journal of Mathematics
Contents
Arnold Kowalski, Institute of Mathematics, University of Szczecin, Wielkopolska 15,
Szczecin 70-451, Poland (arnold.kowalski@usz.edu.pl), and Ivan I. Marchenko,
Institute of Mathematics, University of Szczecin, Wielkopolska 15, Szczecin 70-451,
Poland (iwan.marczenko@usz.edu.pl).
On Shea estimate for deviation of minimal surfaces, pp. 725–740.
ABSTRACT. This paper is devoted to the development of Beckenbach’s theory of
meromorphic minimal surfaces. We get the sharp estimate of Petrenko’s deviation β(a,S)
of meromorphic minimal surface (m.m.s.) S in terms of Valiron’s defect Δ(a,S).
This result is a generalization of the Shea’s result for meromorphic functions
to the case of m.m.s. We also give an example showing that the estimate is
sharp.
Yan Yang, School of Mathematics (Zhuhai), Sun Yat-Sen University, Zhuhai 519082,
China (yangyan8@mail.sysu.edu.cn).
Left eigenvalues and Hamilton-Cayley theorem of matrix in Clifford algebra setting, pp.
741–757.
ABSTRACT. In this paper, we investigate the problems of the left eigenvalues of 2 × 2
matrices A in Clifford algebra setting Rm. Firstly, we prove the existence of the left
eigenvalues for a 2 × 2 matrix in R1m and a special kind of 2 × 2 matrix in Rm. We also
give a method to get left eigenvalues for them. Secondly, we give the definition of
characteristic polynomials of A. Then the Hamilton-Cayley theorem is proved. Finally,
several examples are presented.
D. X. Li, College of Mathematical Sciences, Xiamen University, Xiamen 361005,
Fujian Province, P. R. China (duoxinli52math@163.com), W. C. Lin, Fujian
Preschool Education College, Fuzhou 350007, Fujian Prov-ince, P. R. China
(wclin936@163.com), and A. D. Wu, College of Computer and Information Sciences,
Fujian Agriculture and Forestry University, Fuzhou 350002, Fujian Province, P. R. China
(wadlrr@163.com).
Uniqueness of differential-difference equation on sharing values, pp. 759–783.
ABSTRACT. In this article, we study the uniqueness of differential polynomials of
meromorphic functions with its shift of hyper-order less than 1. We prove three
uniqueness theorems for differential polynomials of meromorphic functions satisfying the
condition of sharing values partially with its shift, extend the result obtained by X. G.
Qi, N. Li and L. Z. Yang.
Kulandhivel Karthikeyan, Department of Mathematics, KPR Institute of Engineering
and Technology, Coimbatore-641407, Tamil Nadu, India (karthi_phd2010@yahoo.co.in),
Gobi Selvaraj Murugapandian, Department of Mathematics, Nandha Engineering
College, Erode-638052, Tamil Nadu, India (murugapandian.g.s@gmail.com), and Ozgur
Ege, Department of Mathematics, Ege University, Bornova, Izmir, 35100, Turkey
(ozgur.ege@ege.edu.tr).
Existence and uniqueness results for sequential ψ-Hilfer impulsive fractional differential
equations with multi-point boundary conditions, pp. 785–805.
ABSTRACT. In this paper, we study multi-point boundary value problems for
sequential impulsive fractional differential equations involving ψ-Hilfer fractional
derivative. Existence and uniqueness results are obtained by using the classical
fixed point theorems of Banach, Krasnoselskii, and the nonlinear alternative of
Leray-Schauder. Some examples are also presented to support our main results.
Liang–Xue Peng, Department of Mathematics, Faculty of Science, Beijing University
of Technology, Beijing 100124, China (pengliangxue@bjut.edu.cn), and Huan Wang,
Department of Mathematics, Faculty of Science, Beijing University of Technology,
Beijing 100124, China (1157569097@qq.com).
On spaces with a σ-NSR pair-base and related conclusions, pp. 807–825.
ABSTRACT. In this article, we first give an equivalent condition for spaces with a
σ-NSR pair-base. Then we introduced a notion of strong NZ(κ)-property, where κ
is a cardinal. We show that a space X has a σ-NSR pair-base if and only if
X satisfies strong NZ(ω)-property. Every space with a σ-point-finite base has
a σ-NSR pair-base. A countable product of spaces with a σ-NSR pair-base
(property (σ-A), property (σ-B)) has a σ-NSR pair-base (property (σ-A), property
(σ-B)).
We give an example to show that NZ(ω)-property does not imply NZ-property. We
give a space which has property (σ-B), but it does not have the Collins-Roscoe property.
We point out that there exists a space which has the NZ(ω)-property, but it does not
have a σ-NSR pair-base. These are complementary for results in [19] and answer a
question which is under Diagram 48 in [19].
Jing Lu, School of Mathematics and Statistics, Shaanxi Normal University, Xi’an
710119, Shaanxi, P.R. China (lujing0926@126.com), Kaiyun Wang, School of
Mathematics and Statistics, Shaanxi Normal University, Xi’an 710119, Shaanxi, P.R.
China (wangkaiyun@snnu.edu.cn), Guohua Wu, Division of Mathematical Sciences,
School of Physical and Mathematical Sciences, Nanyang Technological University,
637371, Singapore (guohua@ntu.edu.sg), and Bin Zhao, School of Mathematics
and Statistics, Shaanxi Normal University, Xi’an 710119, Shaanxi, P.R. China
(zhaobin@snnu.edu.cn).
Nonexistence of k-bounded sobrification, pp. 827–842.
ABSTRACT. In this paper, we will focus on k-bounded sober spaces and show that
every T0 space which is non k-bounded sober admits no k-bounded sobrification. This
strengthens a result of Zhao, Lu and Wang, who proved that the canonical k-bounded
sobrification does not exist. Our work provides a complete solution to a question of Zhao
and Ho, and shows that unlike Sob and BSob, the category KBSob of all k-bounded
sober spaces is not a reflective subcategory of the category Top0 of all T0 spaces.
Furthermore, we introduce the notion of qk-bounded sober spaces and prove that the
category KBSob is a full reflective subcategory of the category QKBSob of all
qk-bounded sober spaces and continuous mappings preserving existing irreducible
suprema.
Chong Shen, School of Science, Beijing University of Posts and Telecommunications,
Beijing, China (shenchong0520@163.com), Xiaoyong Xi, School of Mathematics and
Statistics, Yancheng Teachers University, Yancheng, Jiangsu, China (xixy@yctu.edu.cn),
and Dongsheng Zhao, Mathematics and Mathematics Education, National Institute of
Education, Nanyang Technological University, 1 Nanyang Walk, Singapore 637616
(dongsheng.zhao@nie.edu.sg).
The non-reflectivity of open well-filtered spaces via b-topology, pp. 843–854.
ABSTRACT. Results have shown that Skula’s b-topology plays a core role in studying
sober spaces (especially in studying the sobrification). In this paper, following Skula’s
method of b-embedding a subcategory into the category Top of all topological spaces, we
restrict our attention to T0 spaces, and mainly prove that if K is a reflective subcategory
of the category Top0 of all T0 spaces such that K contains a non-T1 space, then (i) each
K-reflection is a b-dense embedding; (ii) K is saturated-hereditary. As a corollary, we
deduce that the category Owf of all open well-filtered spaces is not reflective in
Top0, which demonstrates a new approach to the reflectivity of subcategories of
Top0.
Mario Eudave-Muñoz, Instituto de Matemáticas, Universidad Nacional
Autónoma de México, Ciudad Universitaria, 04510 Ciudad de México, México
(mario@matem.unam.mx), Araceli Guzmán-Tristán, Centro de Investigación en
Matemáticas, A.C. 402, 36000 Guanajuato, Gto., México (araceli.guzman@cimat.mx),
and Enrique Ramírez-Losada, Centro de Investigación en Matemáticas, A.C.
402, 36000 Guanajuato, Gto., México (kikis@cimat.mx).
On non almost-fibered knots, pp. 855–881.
ABSTRACT. An almost-fibered knot is a knot whose complement possesses a circular
thin position in which there is one and only one thick surface, which is a weakly
incompressible Seifert surface, and one and only one thin surface, which is an
incompressible Seifert surface. Infinite examples of almost-fibered knots are known. In
this article, we show the existence of infinitely many hyperbolic genus one knots that are
not almost-fibered.
Kazuhiro Kawamura, Department of Mathematics, Univesiry ot Tsukuba, Tsukuba,
Ibaraki 305-8571, Japan (kawamura@math.tsukuba.ac.jp).
Interval exchange transformations and shift maps on generalized inverse limit spaces, pp.
883–895.
ABSTRACT. For a generalized interval exchange transformation (in the
sense of Shultz) T : [0,1) → [0,1), there associates an upper semi-continuous
multivalued map T : [0,1] → 2[0,1], for which a two-sided generalized inverse limit
space (in the sense of Mahavier) 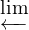 ℤ([0,1],T) and its shift homeomorphism
S :
ℤ([0,1],T) and its shift homeomorphism
S : 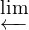 ℤ([0,1],T) →
ℤ([0,1],T) →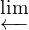 ℤ([0,1],T) are naturally defined. On the other hand, a
construction due to Keane and Shultz gives a homeomorphism σ : X → X of a compact
totally ordered metrizable space X whose dynamics is closely related to that of
T. We prove that, if T satisfies an “aperiodic condition,” then the dynamical
system (
ℤ([0,1],T) are naturally defined. On the other hand, a
construction due to Keane and Shultz gives a homeomorphism σ : X → X of a compact
totally ordered metrizable space X whose dynamics is closely related to that of
T. We prove that, if T satisfies an “aperiodic condition,” then the dynamical
system (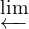 ℤ([0,1],T),S) is topologically conjugate to (X,σ). The result is
regarded as a generalization of a previous construction of J. Kennedy and the
author.
ℤ([0,1],T),S) is topologically conjugate to (X,σ). The result is
regarded as a generalization of a previous construction of J. Kennedy and the
author.
Rongrong Jin, Department of Mathematics, Civil Aviation University of China,
Tianjin, 300300 (rrjin@cauc.edu.cn).
Symmetrical symplectic capacity of coisotropic submanifolds in ℝ2n, pp. 897–921.
ABSTRACT. In this article, we add symmetrical conditions on coisotropic submanifolds
of contact type in real symplectic manifolds. For linear anti-symplectic involution, we
show that the symmetrical Ekeland-Hofer capacities of coisotropic submanifolds
which are of symmetrical contact type in standard linear symplectic space are
positive. Furthermore, for complex projective space and the anti-symplectic
involution induced by conjugation, every coisotropic submanifold which is of
symmetrical contact type and both itself and its complement in the complex
projective space intersect with the real projective space, possesses a noncontractible
symmetrical loop lying on one leaf. In particular, we get that for every hypersurface
which intersects the real projective space transversally and is of symmetrical
contact type in complex projective space, there is a brake closed characteristic on
it.
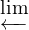 ℤ([0,1],T) and its shift homeomorphism
S :
ℤ([0,1],T) and its shift homeomorphism
S : 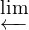 ℤ([0,1],T) →
ℤ([0,1],T) →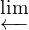 ℤ([0,1],T) are naturally defined. On the other hand, a
construction due to Keane and Shultz gives a homeomorphism σ : X → X of a compact
totally ordered metrizable space X whose dynamics is closely related to that of
T. We prove that, if T satisfies an “aperiodic condition,” then the dynamical
system (
ℤ([0,1],T) are naturally defined. On the other hand, a
construction due to Keane and Shultz gives a homeomorphism σ : X → X of a compact
totally ordered metrizable space X whose dynamics is closely related to that of
T. We prove that, if T satisfies an “aperiodic condition,” then the dynamical
system (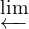 ℤ([0,1],T),S) is topologically conjugate to (X,σ). The result is
regarded as a generalization of a previous construction of J. Kennedy and the
author.
ℤ([0,1],T),S) is topologically conjugate to (X,σ). The result is
regarded as a generalization of a previous construction of J. Kennedy and the
author.