HOUSTON JOURNAL OF
MATHEMATICS
Electronic Edition Vol. 50, No. 1, 2024
Editors: D. Bao (San Francisco, SFSU), S. Berhanu (Temple), D. Blecher
(Houston), B. G. Bodmann (Houston), H. Brezis (Paris and Rutgers),
B. Dacorogna (Lausanne), M.
Gehrke (LIAFA, Paris7), R. M. Hardt (Rice), S. Harvey (Rice), A. Haynes (Houston), Y. Hattori
(Matsue, Shimane), W. B. Johnson (College Station), H. Koivusalo (Bristol), M. Marsh (Sacramento), M. Rojas (College Station),
Min Ru (Houston), S.W. Semmes (Rice), D. Werner (FU Berlin).
Managing Editors: B. G. Bodmann and A. Haynes (Houston)
Houston Journal of Mathematics
Contents
Nilofer Shaikh, Department of Mathematics, University of Mumbai, Mumbai-400098,
Maharashtra, India (shaikhnilofer23@gmail.com), and Rajendra P. Deore, Department
of Mathematics, University of Mumbai, Mumbai-400098, Maharashtra, India
(rpdeore@gmail.com).
On strongly n-absorbing primary ideals, pp. 1–11.
ABSTRACT. Let R be a commutative ring with 1≠0 and n be a positive integer. In
this paper, we introduce the concept of strongly n-absorbing primary ideal.
A proper ideal I of R is called a strongly n-absorbing primary ideal of R if
whenever I1 In+1 ⊆ I for ideals I1,…,In+1 of R, then either I1
In+1 ⊆ I for ideals I1,…,In+1 of R, then either I1 In ⊆ I
or a product of some n of the Ii′s (other than I1
In ⊆ I
or a product of some n of the Ii′s (other than I1 In) is contained in
In) is contained in 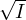 .
We prove some characterizations of n-absorbing primary ideals and strongly
n-absorbing primary ideals. We also prove that these two concepts are equivalent in
u-rings.
.
We prove some characterizations of n-absorbing primary ideals and strongly
n-absorbing primary ideals. We also prove that these two concepts are equivalent in
u-rings.
Philippe Rukimbira, Florida International University, Miami, Florida 33199, USA
(rukim@fiu.edu).
Generalized Eta-Einstein and (κ,μ)-structures, pp. 13–28.
ABSTRACT. It is well known that generalized (κ,μ)- structures occur in dimension 3
only. In this paper, we prove that, in this dimension 3, only K-contact structures can
occur as generalized Eta-Einstein. We also prove that on closed manifolds, Eta-Einstein,
K-contact structures which are not D-homothetic to K-contact Einstein structures are
almost regular. We conclude the paper by constructing examples of compact, generalized
Jacobi (κ,μ)-structures.
C. H. Namitha, The Institute of Mathematical Sciences, A CI of Homi Bhabha
National Institute, 4th cross street, CIT Campus, Taramani, Chennai, India, 600113
(namithachanguli7@gmail.com), and S. Sundar, The Institute of Mathematical
Sciences, A CI of Homi Bhabha National Institute, 4th cross street, CIT Campus,
Taramani, Chennai, India, 600113 (sundarsobers@gmail.com).
Multiparameter decomposable product systems, pp. 29–82.
ABSTRACT. Arveson proved that a 1-parameter decomposable product system is
isomorphic to the product system of a CCR flow. We show that the structure of a generic
decomposable product system, over higher dimensional cones, is given by an isometric
representation V of the cone and a certain 2-cocycle for V . Moreover, we compute the
space of 2-cocycles, modulo coboundaries, for shift semigroups associated to transitive
actions of a higher dimensional cone.
Dongmei Wei, Institute of Mathematics, School of Mathematics, Nanjing Normal
University, Nanjing 210023, P.R.China (weidmei@yeah.net), and Yan Xu, Institute of
Mathematics, School of Mathematics, Nanjing Normal University, Nanjing 210023,
P.R.China (xuyan@njnu.edu.cn).
Montel’s criterion and shared a set of functions, pp. 83–92.
ABSTRACT. Let ℱ be a family of meromorphic functions defined in a domain D, and
ψ(z) be a meromorphic function such that ψ(z)≢0,∞ in D. In this paper, we prove that:
if (1) for each pair of functions f,g ∈ℱ, f and g share the set S = {0,∞,ψ(z)} in D; (2)
the multiplicity of f ∈ℱ is larger than that of ψ at the common zeros or poles of f and
ψ in D, then ℱ is normal in D. Our results improve and generalize Montel’s
normality criterion, and the related results due to Sun-Liu, Charak-Singh, and
Chang-Fang-Zalcman, respectively. Some examples are given to show the sharpness of
our results.
Nan Wang, 1. School of Mathematics, Jilin University, No.2699 Qianjin Street,
Changchun City, 130012, Jilin Province, China. 2. School of Statistics and Data
Science, Zhuhai College of Science and Technology, No.8 Anji East Road, Zhuhai
City, 519041, Guangdong Province, China (wangnanchaos@126.com), Lixin
Jiao, School of Statistics and Data Science, Zhuhai College of Science and
Technology, No.8 Anji East Road, Zhuhai City, 519041, Guangdong Province, China
(jlxchaos@126.com), Lidong Wang, School of Statistics and Data Science, Zhuhai
College of Science and Technology, No.8 Anji East Road, Zhuhai City, 519041,
Guangdong Province, China (wld0707@126.com), and Shaoyun Shi School of
Mathematics and State Key Laboratory of Automotive Simulation and Control, Jilin
University, No.2699 Qianjin Street, Changchun City, 130012, Jilin Province, China.
(shisy@jlu.edu.cn).
Various shadowing properties of iterated function systems, pp. 93–108.
ABSTRACT. Put (X,d) be a compact metric space and f0,f1 be continuous maps
on X. Iterated function systems IFS(f0,f1) is the action of the semi-group
generated by f0,f1 on X. In this paper, we define the d-shadowing property,
chain-ergodic, and the specification property of IFS(f0,f1). Then we show that (1)
IFS(f0,f1) has the average shadowing property, then IFS(f0,f1) has the
d-shadowing property (respectively d-shadowing property); (2) IFS(f0,f1) has the
d-shadowing property (respectively d-shadow-ing property) and f0 or f1 is surjective,
then IFS(f0,f1) is chain-ergodic; (3) IFS(f0,f1) has asymptotic average
shadowing property, if S ⊂ X is dense in X and s is a quasi-weakly almost periodic
point of f0 or f1 for any s ∈ S, then IFS(f0,f1) is ergodic. (4) For a system
IFS(f0,f1) equipped with asymptotic average shadowing proper, where f0,f1 are
open feeble open maps, if S is dense in X and s is a minimal point of f0 or
f1 for any s ∈ S, then IFS(f0,f1) is strongly ergodic. (5) IFS(f0,f1) has
the shadowing property and is mixing, then IFS(f0,f1) has the specification
property.
Yingcui Zhao, School of Computer Science and Technology, Dongguan University of
Technology, No.1 Daxue Road, Dongguan City, 523808, Guangdong Province, China
(zycchaos@126.com).
Distributional chaos and non-wandering point for maps on G-spaces, pp. 109–120.
ABSTRACT. We introduce the definitions of (strong) non-wandering point and
distributional chaos for the map f on G-spaces and show (strong) non-wandering point
(respectively, distributional chaos) implies G-(strong) non-wandering point (respectively,
G-distributional chaos). However, the converse is not true. If f is a pseudo-equivariant
continuous map, then G-(strong) non-wandering set is invariable for f. What’s more, the
condition that f is pseudo-equivariant is essential and cannot be removed. If f has a
G-distributively chaotic pair, then G-strong non-wandering set contains at least two
points. Lastly, we give a sufficient condition for f to be G-distributively chaotic along a
sequence.
Pigar Biteng, School of Mathematical and Statistical Sciences, The University of Texas
Rio Grande Valley, 1201 West University Drive, Edinburg, TX 78539-2999, USA
(pigar.biteng01@utrgv.edu), Mathieu Caguiat, School of Mathematical and Statistical
Sciences, The University of Texas Rio Grande Valley, 1201 West University Drive,
Edinburg, TX 78539-2999, USA (mathieu.caguiat01@utrgv.edu), Dipok Deb, School of
Mathematical and Statistical Sciences, The University of Texas Rio Grande Valley, 1201
West University Drive, Edinburg, TX 78539-2999, USA (dipok.deb01@utrgv.edu),
Mrinal Kanti Roychowdhury, School of Mathematical and Statistical Sciences, The
University of Texas Rio Grande Valley, 1201 West University Drive, Edinburg, TX
78539-2999, USA (mrinal.roychowdhury@utrgv.edu), and Beatriz Vela Villanueva,
School of Mathematical and Statistical Sciences, The University of Texas Rio
Grande Valley, 1201 West University Drive, Edinburg, TX 78539-2999, USA
(betyvelav@gmail.com).
Constrained quantization for a uniform distribution, pp. 121–142.
ABSTRACT. Constrained quantization for a Borel probability measure refers to the
idea of estimating a given probability by a discrete probability with a finite
number of supporting points lying on a specific set. The specific set is known
as the constraint of the constrained quantization. A quantization without a
constraint is known as an unconstrained quantization, which traditionally in
the literature is known as quantization. Constrained quantization has recently
been introduced by Pandey and Roychowdhury. In this paper, for a uniform
distribution with support lying on a side of an equilateral triangle, and the
constraint as the union of the other two sides, we obtain the optimal sets of n-points
and the nth constrained quantization errors for all positive integers n. We also
calculate the constrained quantization dimension and the constrained quantization
coefficient.
Qianshun Cui, School of Mathematics and Statistics, Zhengzhou University, Zhengzhou
450001, People’s Republic of China. (cuiqszzu@163.com), Zejun Hu, School of
Mathematics and Statistics, Zhengzhou University, Zhengzhou 450001, People’s Republic
of China. (huzj@zzu.edu.cn), and Zeke Yao, School of Mathematical Sciences,
South China Normal University, Guangzhou 510631, People’s Republic of China
(yaozkleon@163.com).
Real hypersurfaces in ℂH2 with constant Reeb sectional curvature, pp. 143–156.
ABSTRACT. We show that, contrary to the complex projective plane ℂP2 for which all
the real hypersurfaces with constant Reeb sectional curvature are Hopf ones, there do
exist non-Hopf hypersurfaces in the complex hyperbolic plane ℂH2 with constant Reeb
sectional curvature. Moreover, every non-Hopf hypersurfaces in ℂH2 with constant Reeb
sectional curvature can be constructed by using cohomogeneity two polar actions of
ℂH2.
Bence Horváth, Baloise Insurance Ltd, Aeschengraben 21, Postfach 2275, Basel
4002, Switzerland (hotvath@gmail.com), and Niels Jakob Laustsen, School of
Mathematical Sciences, Fylde College, Lancaster University, Lancaster LA1 4YF, United
Kingdom (n.laustsen@lancaster.ac.uk).
Kernels of operators on Banach spaces induced by almost disjoint families, pp.
157–171.
ABSTRACT. Let 𝒜 be an almost disjoint family of subsets of an infinite set Γ, and
denote by X𝒜 the closed subspace of ℓ∞(Γ) spanned by the indicator functions of
intersections of finitely many sets in 𝒜. We show that if 𝒜 has cardinality greater
than Γ, then the closed subspace of X𝒜 spanned by the indicator functions of sets of the
form ⋂
j=1n+1Aj, where n ∈ ℕ and A1,…,An+1 ∈𝒜 are distinct, cannot be the kernel of
any bounded operator X𝒜→ ℓ∞(Γ). As a consequence, we deduce that the
subspace
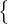 x ∈ ℓ∞(Γ) : x ∈ ℓ∞(Γ) : | the set {γ ∈ Γ : |x(γ)| > 𝜀} has cardinality smaller than Γ for every 𝜀 > 0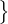 | | |
of ℓ∞(Γ) is not the kernel of any bounded operator on ℓ∞(Γ); this generalises results
of Kalton and of Pełczyński and Sudakov.
The situation is more complex for the Banach space ℓ∞c(Γ) of countably supported,
bounded functions defined on an uncountable set Γ. We show that it is undecidable in
ZFC whether every bounded operator on ℓ∞c(ω1) which vanishes on c0(ω1)
must vanish on a subspace of the form ℓ∞c(A) for some uncountable subset A
of ω1.
K. A. Draziotis, School of Informatics, Aristotle University of Thessaloniki, Greece
(drazioti@csd.auth.gr).
Descent methods for studying integer points on yp = f(x)g(x), for p odd prime, pp.
173–182.
ABSTRACT. We study the integer points on superelliptic curves of the form
yp = f(x)g(x), deg f + deg g ≥ 4 and p odd prime. Based on our method, we provide as
an example the practical solution for the Diophantine equations yp = (Axp + B)g(x) and
yp = (xα + B)(xα + C).
Patricia Pellicer-Covarrubias, Departamento de Matemáticas, Facultad de Ciencias,
Circuito Exterior s/n, Ciudad Universitaria, UNAM, México, CDMX, 04510, Mexico
(paty@ciencias.unam.mx).
Coselectibility regarding symmetric products, pp. 183–214.
ABSTRACT. In this paper we consider a concept defined by Nadler which is the dual to
the concept of a selectible space, namely, a Λ-coselection space (Λ may be any given
hyperspace of a space X). We investigate the concept when Λ is the nth symmetric
product Fn(X). We characterize F2-coselection spaces among a particular class of local
dendrites. We also determine several sufficient conditions for a space X to be an
F3-coselection space.
Félix Capulín, Facultad de Ciencias, Universidad Autónoma del Estado
de México, Instituto Literario 100, Col. Centro, Toluca, CP 50000, México
(fcp@uaemex.mx, fcapulin@gmail.com), Yolanda García, Facultad de Ciencias,
Universidad Autónoma del Estado de México, Instituto Literario 100, Col. Centro,
Toluca, CP 50000, México (fgarciaa754@alumno.uaemex.mx, maffei_yo@hotmail.com),
David Maya, Facultad de Ciencias, Universidad Autónoma del Estado de México,
Instituto Literario 100, Col. Centro, Toluca, CP 50000, México (dmayae@uaemex.mx,
dmayae@outlook.com), and Fernando Orozco-Zitli, Facultad de Ciencias, Universidad
Autónoma del Estado de México, Instituto Literario 100, Col. Centro, Toluca, CP
50000, México (forozco@uaemex.mx, forozcozitli@gmail.com).
Dynamical properties of upper semicontinuous functions, pp. 215–236.
ABSTRACT. Let 2X be the hyperspace of all non-empty closed subsets of a compact
metric space X. A function f from a compact metric space X into 2X is upper
semicontinuous if the set {(x,y) ∈ X × X : y ∈ f(x)} is a closed subset of X × X.
In the current paper, a dynamical system consists of a compact metric space
X and a upper semicontinuous function from a X into 2X. We present some
dynamical properties for this version of dynamical system and we determine
some conditions under which a dynamical system possesses each one of them.
 In+1 ⊆ I for ideals I1,…,In+1 of R, then either I1
In+1 ⊆ I for ideals I1,…,In+1 of R, then either I1 In ⊆ I
or a product of some n of the Ii′s (other than I1
In ⊆ I
or a product of some n of the Ii′s (other than I1 In) is contained in
In) is contained in 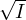 .
We prove some characterizations of n-absorbing primary ideals and strongly
n-absorbing primary ideals. We also prove that these two concepts are equivalent in
u-rings.
.
We prove some characterizations of n-absorbing primary ideals and strongly
n-absorbing primary ideals. We also prove that these two concepts are equivalent in
u-rings.