Editors: D. Bao (San Francisco, SFSU), S. Berhanu (Temple), D. Blecher
(Houston), B. G. Bodmann (Houston), H. Brezis (Paris and Rutgers),
B. Dacorogna (Lausanne), M.
Gehrke (LIAFA, Paris7), R. M. Hardt (Rice), S. Harvey (Rice), A. Haynes (Houston), Y. Hattori
(Matsue, Shimane), W. B. Johnson (College Station), H. Koivusalo (Bristol), M. Marsh (Sacramento), M. Rojas (College Station),
Min Ru (Houston), S.W. Semmes (Rice), D. Werner (FU Berlin).
Managing Editors: B. G. Bodmann and A. Haynes (Houston)
Houston Journal of Mathematics
Contents
Eddie Rohr, Department of Mathematics, 177 College Ave, Tufts University, Medford,
MA 02155 (edward.rohr@tufts.edu), Karthik Sellakumaran Latha, Department of
Mathematics, 520 Portola Plaza, University of California, Los Angeles, CA 90095
(karthiks@math.ucla.edu), and Amanda Yin, Department of Mathematics, University
of Texas at Austin (amandayin@utexas.edu).
A Type D asymmetric simple exclusion process generated by an explicit central element
of 𝒰q(𝔰𝔬10), pp. 237–257.
ABSTRACT. The Type D asymmetric simple exclusion process (Type D ASEP) with
parameters (q,n,δ) is a two-species interacting particle system exhibiting a drift, where
two particles may occupy the same site only if they belong to different species. In
previous research by Kuan, Landry, Lin, Park, and Zhou, the Type D ASEP was
generated using the quantum Hamiltonian corresponding to central elements from the
quantum groups 𝒰q(𝔰𝔬6) and 𝒰q(𝔰𝔬8). We extend this construction to the case of
𝒰q(𝔰𝔬10). Additionally, we generalize a previously known duality function from
Blyschak, Burke, Kuan, Li, Ustilovsky, and Zhou for the Type D ASEP for all
n.
Efstathios-K. Chrontsios-Garitsis, Department of Mathematics, University of
Tennessee, Knoxville, 1403 Circle Dr, Knoxville, TN 37966, USA (echronts@utk.edu),
and Sascha Troscheit, Department of Mathematics, Uppsala University, Box 480, 751
06 Uppsala, Sweden (sascha.troscheit@math.uu.se).
Minkowski weak embedding theorem, pp. 259–273.
ABSTRACT. A well-known theorem of Assouad states that metric spaces satisfying the
doubling property can be snowflaked and bi-Lipschitz embedded into Euclidean spaces.
Due to the invariance of many geometric properties under bi-Lipschitz maps, this result
greatly facilitates the study of such spaces. We prove a non-injective analog of this
embedding theorem for spaces of finite Minkowski dimension. This allows for
non-doubling spaces to be weakly embedded and studied in the usual Euclidean setting.
Such spaces often arise in the context of random geometry and mathematical physics
with the Brownian continuum tree and Liouville quantum gravity metrics being
prominent examples.
Canhui Lu, Department of Mathematics, Sun Yat-sen University, Guangzhou,
Guangdong, 510275, P. R. China (luch37@mail2.sysu.edu.cn), and Xingdi Chen,
Department of Mathematics, Huaqiao University, Quanzhou, Fujian 362021, P. R. China
(chxtt@hqu.edu.cn).
The ramification of holomorphic maps over hypersurfaces on an open Riemann surface
with a conformal metric, pp. 275–289.
ABSTRACT. In this paper, we build a Picard type theorem on an open Riemann surface S with conformal metric
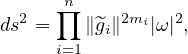
where ω is a holomorphic 1-form, for each i ∈{1,…,n}, gi is a holomorphic map from S into complex projective space ℙm(ℂ), which is ramified over a family of hypersurfaces located in general position.
Lei Shi, School of Mathematical Sciences, Guizhou Normal University, Guiyang 550025,
P. R. China (sishimath2012@163.com).
A note on the generalization of second main theorem for hypersurfaces in subgeneral
position, pp. 291–304.
ABSTRACT. In previous work, we gave an improvement of Schmidt’s subspace type
theorem for hypersurfaces in projective space in subgeneral position. In this paper, we
give a further improvement of its corresponding result in Nevanlinna theory for some
special cases, and we also state analogous result in Diophantine approximation at the end
of this paper.
W. Wang, School of Mathematics, Zhengzhou University of Aeronautics, Zhengzhou
450046, Henan, P. R. China (wangwj072@163.com).
Affine Killing structure vector fields of real hypersurfaces in nonflat complex planes, pp.
305–313.
ABSTRACT. In this paper, we prove that the structure vector field of a real
hypersurface in a nonflat complex plane is affine Killing if and only if it is Killing.
Generalizing this, we prove that the structure vector field of a real hypersurface M in a
nonflat complex plane is η-affine Killing if and only if M is of type (A), (B) or ruled.
These extend main results in [Ki and Kim, Acta Math. Sinica New Ser. 1994] to real
hypersurfaces of any odd dimension.
Ali I. Raad, Mathematics and Science Department, American University in
Bulgaria, Office 307 BAC, ul. Svoboda Bacharova 8, 2700 Blagoevgrad, Bulgaria
(araad@aubg.edu).
C∗-diagonals in AH-algebras arising from generalized diagonal connecting maps:
spectrum and uniqueness, pp. 315–338.
ABSTRACT. We associate a Bratteli-type diagram to AH-algebras arising from
generalized diagonal connecting maps. We use this diagram to give an explicit
description of the connected components of the spectrum of an associated canonical
C∗-diagonal. We introduce a topological notion on these connected components, that of
being spectrally incomplete, and use it as a tool to show how various classes
of AI-algebras, including certain Goodearl algebras and AH-algebra models
for dynamical systems ([0,1],σ), do not admit unique inductive limit Cartan
subalgebras. We focus on a class of spectrally complete C∗-algebras, namely
the AF-algebras, and discuss the uniqueness of their inductive limit Cartan
subalgebras.
Kazuhiro Kawamura, Department of Mathematics, University of Tsukuba, Tsukuba,
Ibaraki 305-8571, Japan (kawamura@math.tsukuba.ac.jp).
Weighted composition operators on Lp-and C0-function spaces over boundaries of
homogeneous trees II, pp. 339–368.
ABSTRACT. As a continuation of a previous paper of the author, we study weighted
composition operators induced by hyperbolic automorphisms on infinite homogeneous
trees and continuous positive weights on the boundaries of these trees. We discuss
disjoint frequent hypercyclicity, existence of common hypercyclic vectors, and the
supercyclicity and its variants for (families of ) such operators. As in the previous paper,
the proof relies on the standard hypercyclicity technique and a combinatorial analysis of
hyperbolic automorphisms on trees.
S. Joseph Lippert, Department of Mathematics and Statistics, Sam Houston State
University.
Refinement of higher-rank graph reduction, pp. 369–397.
ABSTRACT. Given a row-finite, source-free, graph of rank k, we extend the definition
of reduction introduced by Eckhardt et al. This constitutes a large step forward in the
extension of the geometric classification of finite directed graph C∗-algebras presented
by Eilers et al. to higher-rank graph C∗-algebras. This new move acts as an
inverse to delay, directly extends the previous version, and provides previously
undocumented Morita classes of k-graphs. In pursuit of this extension, we formalize what
constitutes a higher-rank graph move. Specifically, we use this formalization as a
bridge between the new geometric reasoning and the classical category theoretic
construction.
Youjun Wang, School of Mathematics and Statistics, Henan University, Kaifeng
475004, P. R. China (math_wyj@henu.edu.cn, math_wangyoujun@163.com).
Fractional moment of symmetric square L-function and its applications, pp.
399–412.
ABSTRACT. Let f be the Hecke eigenform for the modular group SL2(ℤ), L(s,sym2f) the symmetric square L-function related to f. For 1∕2 < σ < 1, define m(σ) as the supremum of all numbers m such that
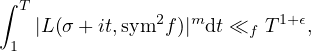
where 𝜖 > 0 is an arbitrarily small number. In this paper, the bound
m(σ) ≥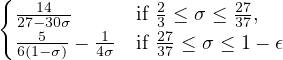 |
is established. Furthermore, as applications, the average behavior of Fourier coefficients of symmetric power L-functions were considered.
Guodong Hua, School of Mathematics and Statistics, Weinan Normal University,
Weinan, Shaaxi Province, China 714099, Research Institute of Qindong
Mathematics, Weinan Normal University, Weinan, Shaaxi Province, China 714099
(gdhuasdu@163.com).
On a certain multidimensional general divisor problem associated to coefficients of
Dedekind zeta function, pp. 413–436.
ABSTRACT. Let τkjKj(n),1 ≤ j ≤ ν,ν ≥ 2 be the kj-dimensional divisor function in
the number field Kj∕ℚ. In this paper, we investigate the asymptotic behaviour of a
multidimensional general divisor problem concerning the product of the higher power
moments of τkjKj(n) involving finitely many distinct number fields over specific
sequences of positive integers under suitable mild conditions. As an application, we also
obtain the corresponding asymptotic formulae of the variance of the sequences of the
same coefficients.
Alejandro Illanes, Instituto de Matemáticas, Universidad Nacional Autónoma de
México, Circuito Exterior, Cd. Universitaria, México 04510, Ciudad de México
(illanes@matem.unam.mx), and Verónica Martínez-de-la-Vega, Universidad
Nacional Autón-oma de México, Circuito Exterior, Cd. Universitaria, México 04510,
Ciudad de México (vmvm@matem.unam.mx).
Arcwise connectedness in hyperspaces of closed totally disconnected subsets, pp.
437–442.
ABSTRACT. Given a topological space X, we consider the hyperspace TD(X) of closed
totally disconnected subsets of X. In this paper we show that on dendroids the
non-uniformly arcwise connectedness is an obstruction for the arcwise connectedness of
TD(X) in X. In fact, we prove that if X is non-uniformly arcwise connected dendroid,
then TD(X) has 𝔠 arc components.
Javier Camargo, Escuela de Matemáticas, Facultad de Ciencias, Universidad
Industrial de Santander, Ciudad Universitaria, Carrera 27 Calle 9, Bucaramanga,
Santander, A. A. 678, Colombia (jcam@matematicas.uis.edu.co), and Sergio Macías,
Instituto de Matemáticas, Universidad Nacional Autónoma de México,
Circuito Exterior, Ciudad Universitaria, México D. F., C. P. 04510, Mexico
(sergiom@matem.unam.mx, macias@unam.mx).
More on quotients of n-fold hyperspaces, pp. 443–475.
ABSTRACT. Let X be a continuum, and let n be an integer greater than or
equal to two. Consider the n-fold hyperspace of X, 𝒞n(X), consisting of all
nonempty closed subsets of X with at most n components. We define the quotient
space 𝒞1n(X) = 𝒞n(X)∕𝒞1(X), with the quotient topology. We call 𝒞1n(X) the
n-fold quotient hyperspace of X. We prove several properties of n-fold quotient
hyperspaces. For example: we present upper bounds of the dimension of the n-fold
quotient hyperspaces for some classes of continua. If X is a locally connected
continuum such that either dim(𝒞n(X)) is finite or does not contain free arcs, then
𝒞1n(X) is an absolute retract. We characterize the unit interval and the simple
closed curve as the only graphs for which the n-fold quotient hyperspaces are
Cantor manifolds. We prove that the n-fold quotient hyperspaces have trivial
shape. Given a map between continua, we define the induced map between the
n-fold quotient hyperspaces and consider the relations between several classes
of maps and the induced maps on n-fold hyperspaces and on n-fold quotient
hyperspaces.
Hualin Miao, School of Mathematics, Hunan University, Changsha, Hunan, 410082,
China (miaohualinmiao@163.com), Xiaodong Jia, School of Mathematics, Hunan
University, Changsha, Hunan, 410082, China (jiaxiaodong@hnu.edu.cn), Ao Shen,
School of Mathematics, Hunan University, Changsha, Hunan, 410082, China
(shenao2020@163.com), and Qingguo Li, School of Mathematics, Hunan University,
Changsha, Hunan, 410082, China (liqingguoli@aliyun.com).
ω-well-filtered spaces revisited, pp. 477–495.
ABSTRACT. We prove that a T0 topological space is ω-well-filtered if and only if it does not admit either the natural numbers with the cofinite topology or with the Scott topology as its closed subsets in the strong topology. Based on this, we offer a refined topological characterization of the ω-well-filterification of T0-spaces and solve a problem posed by Xiaoquan Xu. In the setting of second-countable spaces, we also characterise sobriety by convergences of certain Π20-Cauchy subsets of the spaces.