Overview
I am a member of the
Numerical Analysis and Scientific Computing group.
My research interests lie in the analysis and development of finite element methods with applications to fluid dynamics and nonlinear PDEs with nonlcal diffusive operators.
They include the following areas of research:
- Numerical Analysis and Scientific Computing
- Computational Fluid Dynamics.
- Finite Element Method.
- DG method for flows in porous media.
- Incompressible Navier-Stokes (constant and variable density).
- Maxwell equations.
- Nonlocal Diffusive operators (Gray-Scott model).
- Applications to Magnetohydrodynamics, Thermal convection and Turbulence.
Research grant
- National Science Foundation DMS-2208046 ($170 913, 09/01/2022-08/31/2025)
Project Title: Numerical methods for incompressible multiphase flows applied to magnetohydrodynamics
NSF Announcement: here
Research group at UH
- Graduate students:
- Mark Simmons (Fall 2023-present)
- Salvatore Giordano (Fall 2023-present)
- An Vu (Fall 2021-Summer 2024)
Here is a list of previous members of my research group:
- Postdoctoral Research Associate.
Research projects
The following gives a short description of research projects I am working on.
Incompressible Multiphase flows
Outline.
The approximation of multiphase phase flows problems leads to solving the
Navier-Stokes equations where the fluid properties, such as density and viscosity,
are space and time dependent. To approximate such problems, my research focuses
on the development and analysis of numerical methods that are suitable for finite element and
spectral methods. These methods are implemented in the code SFEMans and
they have been used to study magnetohydrodynamics instabilities
in liquid metal batteries and allumina production cells. Other applications involving
thermodynamics problems are also considered (e.g. liquid metals cooled nuclear reactors).
Graduate Students: An Vu, Salvatore Giordano.
Collaborators. Jean-Luc Guermond (Texas A&M University),
Wietze Herreman (Paris-Saclay University),
Gerrit Maik Horstmann (HZDR, Dresden),
Caroline Nore (Paris-Saclay University)
and Norbert Weber (HZDR Dresden).
Porous media: Black Oil model
Outline.
In the frame of reservoir simulation, I am interested in the approximation of black oil model
where a system is composed of three phase (liquid, vapor, aqueous) and three components
(oil, gas water) in a porous media (reservoir). To handle more easily unstructured mesh
and go toward high order element, we developed a discontinuous Galerkin finite element
method that can deal with highly heterogeneous media and phase appearance/disapearance
without additional effort. The algorithm also allows mass transfer between the liquid and vapor phase
(meaning that the oil and gas can either be in liquid or phase phase).
The method is implemented in the code DUNE and allows us to study problem of oil extraction
and viscous fingers generation.
Graduate Students: Mark Simmons.
Collaborators. Beatrice Riviere (Rice University),
Vivette Girault (Paris VI University)
and Giselle Sosa Jones (Oakland University).
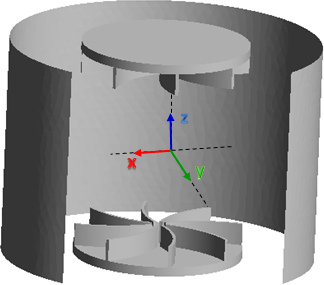
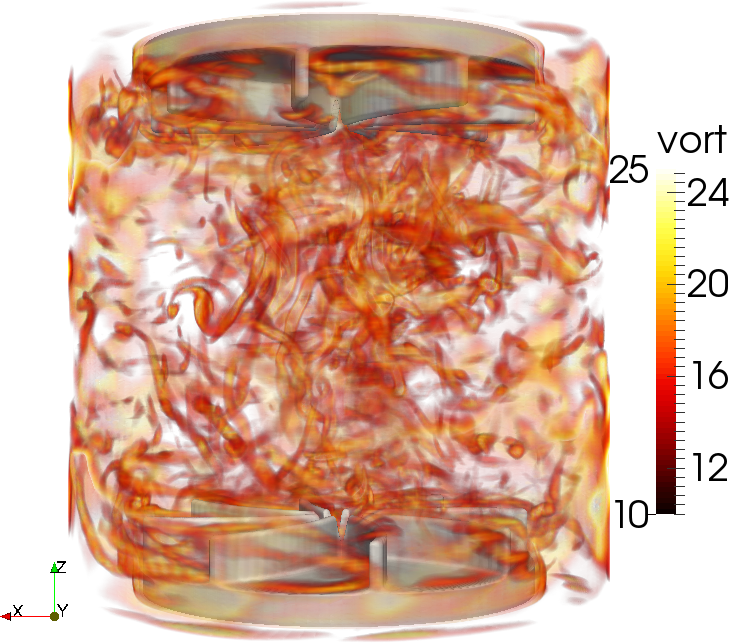
Turbulence and Large Eddy Simulation (LES) model
Outline.
The dynamo effect is the generation and/or the subtain of a magnetic field
from the convertion of the kinetic energy of a conducting fluid into magnetic
energy. This phenomena is important as it is responsible for the presence of
many magnetic field in geophysics (like the one of Earth). To get a better
understanding of the mechanism behing dynamo action, my research focuses
on the numerical study of two experimentals set ups of Von Karman flows (VKS, see right picture).
The two main numerical challenges are to be able to consider moving impellers that
drives the fluid into motion and that dynamo effect only occurs for large Reynolds number
where the flow become turbulent. We faced these difficulties by validating a large eddy simulation
(LES) model based on a entropy stabilization technique and by using a penalty technique to represent
the actions of the impellers.
Collaborators. Daniel Castanon Quiroz (Cote d'Azur University),
Jean-Luc Guermond (Texas A&M University),
Jacques Leorat (LUTH-Observatory of Paris),
and Caroline Nore (Paris-Saclay University).